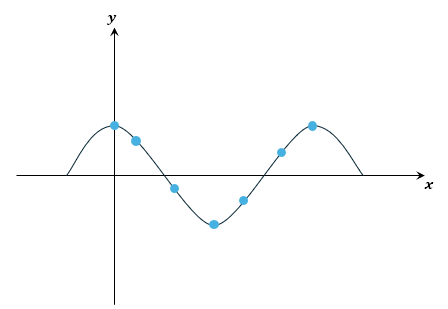
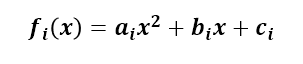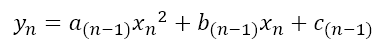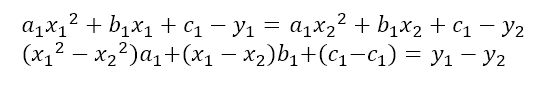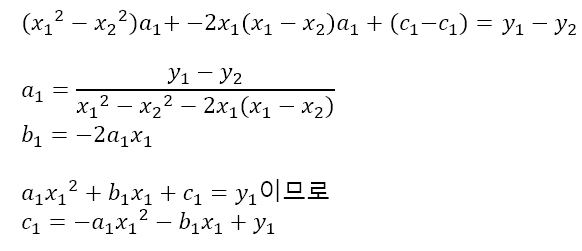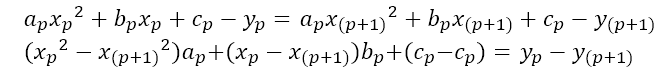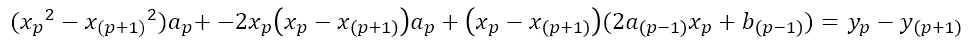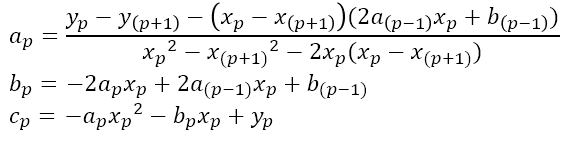이제 스플라인 보간법을 이용하여 점을 잇는 간단한 프로그램을 만들어 보려고 한다.
Qt 프레임워크를 이용, CMake 빌드도구로 만들어보았다.
동작:
마우스의 왼쪽 버튼을 누르면 점이 찍히고, 화면에 3개 이상의 점이 찍히면 점을 찍은 순서대로 잇는다.
마우스의 오른쪽 버튼을 누르면 화면에 그려진 그림을 지운다.
방법:
QWidget의 멤버 함수인 마우스 이벤트 함수(mousePressEvent)를 오버라이드
QTimer의 멤버 함수인 타이머 함수(timerEvent) 오버라이드
QGraphicsScene 변수를 정의하고 addPixmap 함수 input에 QPixmap 그림을 추가하는 방법으로 마우스가 눌릴 때마다 그려지는 그림 변경
.h
멤버 변수는 다음과 같이 정의했다.
bool b_clicked; // 왼쪽 마우스 클릭 플래그
int index; // 화면에 찍힌 점의 개수
QPixmap * Pixmap; // 갱신할 pixmap 이미지
QPoint * Point; // 점의 위치 저장
QGraphicsView * m_view;
QGraphicsScene * m_scene;
.cpp
생성자에 다음과 같이 m_view, m_scene, 점, 이미지 배열을 초기화 하였다.
MainWindow::MainWindow(QWidget *parent)
: QMainWindow(parent)
, ui(new Ui::MainWindow)
{
index = 0;
b_clicked = false;
// m_view에 사용할 장면 설정
this->setCentralWidget(m_view = new QGraphicsView());
m_scene = new QGraphicsScene;
m_view->setScene(m_scene);
m_view->setGeometry(10,30,TILE_WIDTH,TILE_HEIGHT);
// 점, 이미지를 저장할 배열 초기화
Pixmap = new QPixmap[MAXLENGTH];
Point = new QPoint[MAXLENGTH];
QPixmap pixmapWhite(TILE_WIDTH, TILE_HEIGHT);
pixmapWhite.fill(Qt::white); // 띄울 첫 이미지는 하얀 바탕으로 함
Pixmap[0] = pixmapWhite;
this->startTimer(0); // 타이머 시작
}
마우스가 눌릴 때의 이벤트를 처리하는 함수는 왼쪽과 오른쪽 마우스 클릭을 구분할 수 있다.
왼쪽 마우스가 눌렸을 경우 왼쪽 마우스 클릭 플래그 b_clicked를 true로 하고 점의 개수를 카운트하는 index에 1 증가시킨다. mousePressEvent의 매개 변수 event를 통해 왼쪽 마우스가 눌린 위치를 가져와 점 배열에 저장한다.
void MainWindow::mousePressEvent(QMouseEvent * event)
{
// 왼쪽 마우스 클릭
if (event->button() == Qt::LeftButton)
{
b_clicked = true;
Point[index] = event->pos();
index++;
qDebug() << "window value at (" << point.x() << ", " << point.y() << "): " << point;
}
// 오른쪽 마우스 클릭
else if(event->button() == Qt::RightButton)
{
index = 0; // 점 개수 0으로 초기화
QPixmap p(TILE_WIDTH, TILE_HEIGHT);
p.fill(Qt::white);
Pixmap[0] = p;
m_scene->addPixmap(Pixmap[0]);
}
QWidget::mousePressEvent(event);
}
이제 왼쪽 마우스가 클릭 됐음을 인식하여 점과 곡선을 그려주기 위해 timerEvent 함수를 처리할 것이다. (그려지는 동작을 mousePressEvent 함수가 아니라 timerEvent 함수에 처리하는 이유는 추후 다른 옵션을 추가하더라도 timerEvent 함수에서만 수행할 수 있도록 하기 위해서이다. 구현 방법은 다양하므로 각자 상황에 맞는 코드를 짜면 되겠다.)
void MainWindow::timerEvent(QTimerEvent *)
{
if(b_clicked)
{
QPixmap linePix;
QImage img = Pixmap[index - 1].toImage();
// 점 그리기
linePix = generateDot(img, point, 4);
// append it to the buffer
Pixmap[index] = linePix;
if(index >= 3)
{
// 곡선 그리기
linePix = generateCurve(img);
}
m_scene->addPixmap(linePix);
b_clicked = false;
}
}generateCurve 함수는 최소 점이 3개 이상 찍혔을 때 Spline interpolation에 의해 생성된 스플라인 함수를 그리는 역할이다. 점과 곡선을 그린 후, m_scene에 그린 pixmap을 띄우고 왼쪽 마우스 클릭 플래그를 off 한다.
자, 이제 Point에 저장된 점 사이에 생성되는 스플라인 함수를 구해보자. 나의 경우는 재귀함수로 구현했지만, 임베디드 시스템처럼 자원이 제한적인 시스템에서는 재귀함수로 구현하기 보단 배열을 이용하는 방법이 적합할 것이다. 스플라인 함수의 계수를 저장하는 배열을 멤버 변수에 저장하고 계수 저장 배열을 계속해서 검색, 갱신해가며 찾는 방법이 있다.
double * MainWindow::getSplineInterpolation(int n)
{
if(n == 2)
{
// a_1, b_1, c_1 계산
double * para = new double[3];
double dividend = ((double)Point[n - 2].y() - (double)Point[n - 1].y());
double divisor = (pow((double)Point[n - 2].x(), 2) - pow((double)Point[n - 1].x(), 2) - 2 * Point[n - 1].x() * ((double)Point[n - 2].x() - (double)Point[n - 1].x()));
if(divisor == 0)
divisor = 0.0000001;
para[0] = (dividend / divisor);
para[1] = para[0] * (-2) * Point[n - 1].x();
para[2] = Point[n - 2].y() - para[0] * pow(Point[n - 2].x(), 2) - para[1] * Point[n - 2].x();
return para;
}
else
{
// a_n-1, b_n-1, c_n-1 계산
double * prev_para = getSplineInterpolation(n - 1);
double * para = new double[3];
double dividend = (((double)Point[n - 2].y() - (double)Point[n - 1].y())
+ (-2 * prev_para[0] * Point[n - 2].x() - prev_para[1]) * (Point[n - 2].x() - Point[n - 1].x()));
double divisor = (pow(Point[n - 2].x(), 2) - pow(Point[n - 1].x(), 2) -2 * Point[n - 2].x() * (Point[n - 2].x() - Point[n - 1].x()));
if(divisor == 0)
divisor = 0.0000001;
para[0] = (dividend / divisor);
para[1] = 2 * prev_para[0] * Point[n - 2].x() + prev_para[1] -2 * para[0] * Point[n - 2].x();
para[2] = Point[n - 2].y() - para[0] * pow(Point[n-2].x(), 2) - para[1] * Point[n-2].x();
return para;
}
}

앞선 글에서 구한 a_1, b_1, c_1, a_p, b_p, c_p 값이 위와 같음을 이용하였다. (궁금하신 분은 이전의 글을 보면 도움이 될 것이다.)
getSplineInterpolation 함수 내에서 자기 자신을 다시 호출하고, 현재의 점(n)구간보다 1번 더 이른 시점의 점(n-1)구간의 계수를 prev_para에 저장하여 반환한다. prev_para[0], prev_para [1] 값을 이용하여 계수 a_n, b_n을 계산한다.
결과
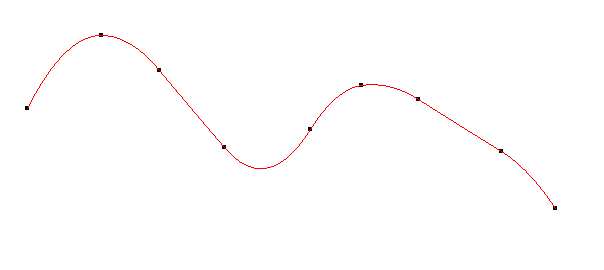
알고리즘을 검증하기 위해 이미 알려져 있는 점에서 알고리즘을 통해 계산한 다항식의 계를 도출해보았다.
| x | y |
| 1 | 5 |
| 2 | 12 |
| 3 | 23 |
x구간 [1, 2]에서의 다항식 계

x구간 [2, 3]에서의 다항식 계

이미 알려진 점에서의 다항식 계와 일치하였다.
고찰
이렇게 하면, getSplineInterpolation 의 계수를 이용하여 1~n까지의 계수를 구할 수 있을 것이다. 사실, 위와 같은 재귀함수 방법으로 구현하는 것은 상당히 비효율적인 방법이라고 할 수 있다. 1번째 스플라인 함수를 구하기 위해 getSplineInterpolation 함수는 1번 호출되고, 2번째 스플라인 함수를 구하기 위해 getSplineInterpolation 함수는 2번 호출되니 말이다. 그럼 n번째 스플라인 함수는 n번 호출된다. 즉, 동일 작업을 반복하고 있는 꼴이다. 이 반복을 피하기 위해 param[3][n] 변수를 정의하고 1번째 스플라인 함수 계수를 0번째 저장, 2번째 스플라인 함수는 param의 0번째 값을 이용하여 1번째에 저장하면 n번째까지 저장할 수 있다.
'프로젝트 > 보간법' 카테고리의 다른 글
| Spline interpolation (스플라인 보간법) 개념 (0) | 2025.03.17 |
|---|