2. 오일러의 공식 증명

: 미분값이 자기 자신인 함수
(자연 상수 e는 무리수이며 순환하지 않는 무한 소수이다)

함수 f(x)의 미분은 다음과 같다.

x변화율, ⊿x를 양변에 곱하면,

f(x)를 양변에 더하면,

이때, 함수 f(x)의 미분값은 자기 자신이므로,

위와 같이 정리할 수 있다.
x에 값을 대입하여 위 공식을 분석해보자.

n⊿x값을 치환해보자.

n⊿x에 x를 대입하면, ⊿x는 0에 가까이 가야하므로 n은 무한대에 가깝게 간다.
대입하여 정리해보자.

f(x)는 무한 항을 가진 무한 차수가 된다.
위 공식을 그래프로 그리면, x가 0일때, 1을 지나며 점근선은 y=0이다.

그렇다면? x에 허수 i를 곱한 e^ix는 어떨까?
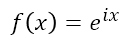
f(x)의 미분은 ...

⊿x를 양변에 곱하면,

f(x)를 양변에 더하면,

이때, 함수 f(x)의 미분값은 허수 i를 곱한 자기 자신이므로,

자, 이제 다시 x에 값을 대입하여 위 공식을 분석해보자.

n⊿x값을 치환하자.


e^x 함수에서 x에 허수를 곱했더니, 실수부, 허수부로 이뤄진 무한 차수가 도출되었다.
이때, x가 1일 때의 함수값을 a+bi라고 하면,

이를 좌표계에 표현하기 위해 허수축을 추가하여 그려보자.
그럼 x=1일때, 실수부는 a, 허수부는 b이므로 다음과 같이 그려진다.

미분 공식에서 유도한 다음과 같은 다항식을 그래프에 표현하여 어떻게 그려지는지 확인해보자.

아래와 같이 x축을 기준으로 바라보는 그래프로 보자.

복소평면과 같은 좌표계가 보이고, 이 좌표계에 f(x) 점을 찍었다.
i⊿xf(x)는 f(x)에 0에 가까이 가는 ⊿x를 곱하여 amplitude가 0에 수렴할 것이고, 허수 i를 곱하여 f(x)와 시계반대방향으로 90º의 각을 이루며 위치할 것이다. 따라서 f(x)와 i⊿xf(x)를 더한 f(x+⊿x)는 다음과 같이 빨간 선으로 그려진다.

그래프에 따르면, f(x)와 i⊿xf(x)는 항상 수직을 이룰것이다. 이 정의로 미루어보아, f(x)는 원의 특성과 일치.
f(x)는 허수축을 추가한 좌표평면을 x축 기준으로 봤을 때 그래프는 원의 형태로 그려진다라는 것을 알 수 있다.
원은 원점에서 원 위의 어느 한 점에 발을 내린 선분과 발을 내린 점의 접선과 항상 수직인 특성을 가지고 있다.


e의 ix승은 x값이 증가함에 따라 실수부, 허수부 사이에서 나선형을 그리는 주기 함수로 그릴 수 있다.
여기서 정말 신기한 부분!
이 함수 e의 ix승의 그래프를
(1) y축으로 볼 때 (말하자면) x축, 허수축 사이에서 그려지는 그래프 모양
(2) 허수축으로 볼 때 (말하자면) x축, y축 사이에서 그려지는 그래프 모양
으로 본다면 쾌감을 느낄 수 있을 것이다.
(1) y축으로 본 그래프 모양

(2) 허수축으로 본 그래프 모양

즉, e의 ix승의 함수의 그래프는 x가 증가함에 따라 반시계방향으로 돌 때, sin파와 cos파의 융합이다.


'프로젝트 > 신호처리' 카테고리의 다른 글
| 오일러의 공식 증명하기 (1. 복소수의 이해) (0) | 2025.03.11 |
|---|






