Spline interpolation (스플라인 보간법) 개념

공학, 과학에서는 다양한 데이터 종류들이 있다. 이와 같은 데이터들은 보통 제한된 수의 데이터들이므로 공학자, 과학자들은 주어진 데이터 사이의 (공백으로 남겨진..) 값을 궁금해한다.

따라서 데이터의 원래 값을 어떻게 하면 최대한 보간할 수 있는지에 대한 방법들에 관심이 많을 수밖에 없다.

자, 그렇다면 아래와 같은 점들을 연속적으로 이어지도록 하려면 어떻게 해야 할까? 

 

방법은 다양하지만 아래 2가지 방법으로 점을 이어보았다.

 

 

각 점을 직선으로만 근사한 이미지를 보면.... 근사한 값의 오차가 클 것임을 알 수 있다. 이는 주어지는 점(정보)의 개수가 적으면 적을수록 이러한 오차가 더욱 크게 나타날 것이다. 

하지만 곡선으로 근사했을 경우 이러한 오차를 줄일 수 있다.

 

곡선 형태의 근사방법에는 여러 방법들이 존재한다. 

예를 들어 다항식 보간법은 N개의 점에 대해 N-1차 다항식으로 보간하는 방법이다. 당연히 1차 다항식으로 보간하는 방법보다 더 높은 차수로 보간하면 오차율이 줄어든다. 더 많은 차수의 항을 포함하므로 원 데이터를 더욱 세밀하게 추적할 수 있기 때문이다. 하지만 너무 큰 차수의 다항식으로 보간하게 되면 오버슈트(overshoot), Runge's phenomenon 현상으로 오히려 오차율이 증가할 수 있다.

(이에 대한 자세한 설명은 신호 처리에 대한 내용을 올릴 때 자세히 적도록 하겠습니다.)

 

Spline interpolation (스플라인 보간법)

스플라인 보간법은 각 점 사이의 구간마다 서로 다른 스플라인 함수를 구성하여 보간하는 방법이다. N개의 점의 N-1개의 구간에서 각 구간마다 스플라인 함수를 가진다.

 

스플라인 보간법은 사용되는 스플라인 함수의 차수에 따라 1차 스프라인 보간법, 2차 스프라인 보간법, 3차 스프라인 보간법이 존재한다. 이 중 2차 스플라인 함수를 구현해보고 간단한 곡선 그리기 프로그램에 Qt로  적용해보려고 한다.

 

2차 스플라인 보간법에서 각 스플라인 함수들은 아래와 같은 함수 형태일 것이다.

N개의 점에서 N-1개의 함수를 가질것이고 함수 당 3개의 미지수가 존재하기 때문에 3×(N-1)개의 미지수가 존재, 3×(N-1)개의 연립방정식이 필요하다.

 

[2차 스플라인 보간법의 규칙]

1. 각 점에서 이웃한 다항식의 함수값은 같아야 한다.
2. 함수는 첫 점과 끝 점을 지나야 한다.
3. 각 점에서 이웃한 1차 도함수는 연속이어야 한다. (이웃한 다항식의 1차 도함수는 같아야 한다.)
4. 첫 구간에서의 도함수는 0이라고 가정한다. 

위의 규칙들을 이용하면 3×(N-1)개의 미지수의 해를 풀 수 있다.

규칙 1번에 의해 2×(N-2)개의 식을 만들 수 있다. (양 끝점을 제외하면 N-2개의 점에서 이웃하는 다항식이 2개 존재하므로)

규칙 2번에 의해 2개의 식을 만들 수 있다. (각 구간의 함수는 첫 점과 끝점 2개의 점을 지나므로)

규칙 3번에 의해 N-2개의 식을 만들 수 있다. (양 끝점을 제외한 도함수는 교점에서 함수값이 동일해야 하므로 N-2개)

규칙 4번에 의해 1개의 식을 만들 수 있다.

따라서 총 3×(N-1)개의 미지수의 해를 풀 수 있다.

 

---

위 조건들을 이용하여 n개의 점이 존재할 경우 f(n-1)(x)함수에 대한 계수 a(n-1) , b(n-1) , c(n-1)을 구해보았다.

총 n개의 점에 대해 n-1개의 스플라인 함수가 존재하므로 위와 같이 표현하였다.

 

규칙 4번에 의해 x1, y1 점에서의 도함수가 0이라고 가정하였다.

 

규칙 1, 2번에 의해

이므로 b1에 -2a1x2를 대입하면,

이렇게 a1, b1, c1에 대한 첫번째 스플라인 함수의 계수를 구하였다.

 

이제 2~n-1의 스플라인 함수를 구할 수 있다.

p가 2보다 크거나 작고 n-1보다 작거나 같을 때, p-1 스플라인 함수의 도함수와 p 스플라인 함수의 도함수는 다음과 같이 표현할 수 있다.

규칙 3번에 의해 

다음과 같은 다항식이 성립한다.

규칙 1번에 의해 

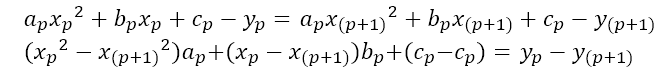
b_p에 -2a_p x_p+2a_((p-1)) x_p+b_((p-1))를 대입하면,

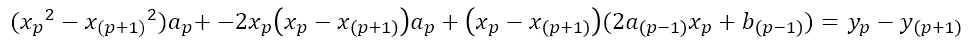
이제, a_p에 대해 정리하면,

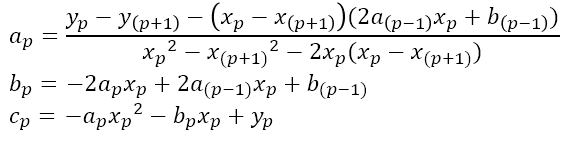
이렇게 첫번째 스플라인 함수의 계수 a1, b1, c1을 먼저 구한 후 이를 이용하여 a_p, b_p, c_p를 구할 수 있다.

(2≤p≤n-1)

 

계수를 구했으니 다음 글은 Qt를 이용하여 spline interpolation에 의해 점을 잇는 프로그램을 만드는 과정을 올릴 것이다.